Enlace Químico ejercicio 32: Demostrar la no existencia del compuesto NaO con el Ciclo de Born Haber

0
30742

Contenido del Vídeo

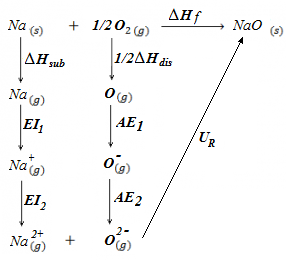
En este ejercicio se pretende justificar, mediante el uso del Ciclo de Born-Haber, la no existencia del óxido de sodio (II), es decir, NaO, con valencia +2 para el átomo de sodio. El enunciado completo es el siguiente:

Justificar, mediante el Ciclo de Born-Haber y los datos aquí indicados, la no existencia del compuesto NaO (Na(+2), O(-2)), suponiendo que su energía reticular fuese del orden de la del óxido de calcio, CaO, -3525 kJ/mol.

EI1 Na = 494 kJ/mol

(primera energía de ionización del sodio, es decir, la energía necesaria para abstraer el electrón de valencia del átomo y quedar como Na+).

EI2 Na = 4561 kJ/mol

(segunda energía de ionización del sodio, energía necesaria para abstraer un segundo electrón del Na+ para que quede como catión divalente, Na(2+)).

AE1 O = -142 kJ/mol

(primera afinidad electrónica del oxígeno, energía desprendida cuando el oxígeno neutro y gaseoso pasa al anión monovalente O(-)).

AE2 O = -791 kJ/mol

(segunda afinidad electrónica del oxígeno, energía desprendida cuando el anión oxígeno monovalente, O(-), pasa a. anión divalente, O(2-), más estable).

ΔH sub Na = 107 kJ/mol

(entalpía de sublimación del sodio, es decir, energía necesaria para pasar de sodio metálico sólido a sodio gaseoso).

ΔH dis O2 = 498 kJ/mol

(entalpía de disociación del oxígeno diatómico, es decir, energía necesaria para romper los enlaces covalentes O-O y tener átomos de oxígeno independientes y gaseosos).

Ciclo de Born-Haber para el monóxido de sodio, NaO